[ 2025 in Review ] Paley-Wiener Type Theorems for Fractional Dirac Operators

In 2025, I’ve strengthened international collaborations with colleagues in Portugal and Germany, making notable contributions to harmonic analysis, hypercomplex variables, and fractional PDEs.

One of his standout publications, “Paley–Wiener Type Theorems Associated to Dirac Operators of Riesz–Feller Type” (J. Fourier Anal. Appl., 31(52), 2025), which I’ve co-authored with Swanhild Bernstein, appeared in a top-tier journal on CIDMA’s Positive Discrimination List. This reflects the quality and significance of this work.

Below, I will make an overview of this selected contribution.

In classical harmonic analysis, the Paley-Wiener theorem is a “perfect” result that connects two seemingly different concepts: the decay of a function in space and the size of its frequency support. Simply put, the theorem states that a function cannot be essentially limited in both time and frequency unless it is identically zero.

For decades, extending this theorem to higher dimensions has relied heavily on complex analysis techniques, such as holomorphic extensions. But what happens when we move to fractional operators in higher dimensions, where traditional complex analytic tools like the Cauchy integral formula don’t apply?

In our latest paper, published in the Journal of Fourier Analysis and Applications (2025), Swanhild Bernstein and I tackle this challenge by introducing a new framework for hypercomplex Paley-Wiener theorems.

The Challenge: Missing Tools

When working with Riesz-Feller type Dirac operators ($D_{\theta }^{\alpha }$), we deal with operators that have a fractional order α, and a skewness, θ. While these are powerful tools for modeling anisotropic diffusion and wave propagation, they render the standard “holomorphic” toolkit typically relied on in Clifford analysis ineffective. We cannot simply extend the function into the complex plane in the traditional sense.

The Solution: Semigroups and Real Methods

Rather than searching for a complex extension, we examined growth behavior. We used the theory of Lévy-Feller semigroups, which are essentially generalized diffusion processes, to replace the missing holomorphic extension.

By defining a new class of generalized Hardy spaces , we successfully proved a “Real Paley-Wiener Theorem.” Our main result establishes an equivalence between three key properties:

1. Compact Support: The Fourier transform of the function is supported in a ball of radius .
2. Bernstein Inequalities: The iterates of our fractional operator satisfy a specific growth bound: .
3. Exponential Type: The solution to the associated Cauchy problem grows no faster than an exponential function of type .

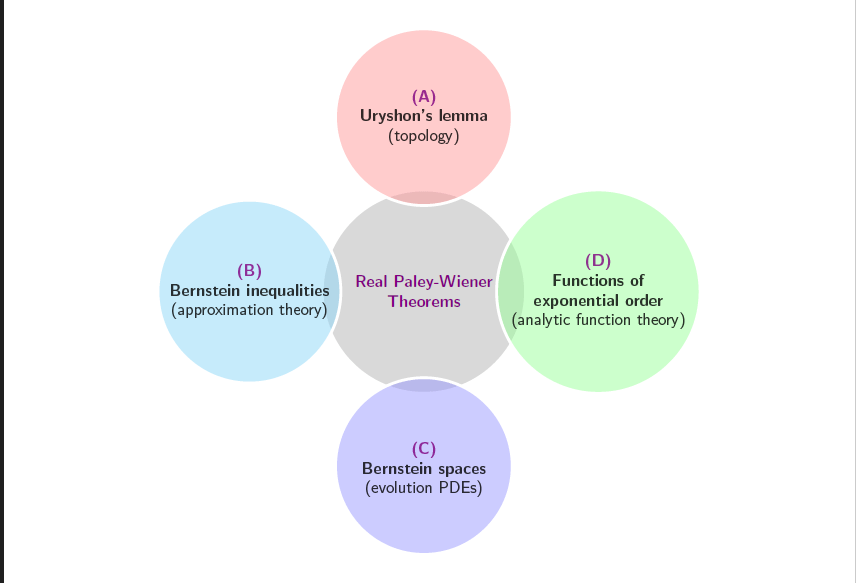
Why It Matters

This result enables us to define Bernstein spaces for fractional operators in higher dimensions rigorously. It provides a precise, mathematical description of “band-limited” signals in complex, multidimensional systems, eliminating the need to force the problem into a classical, complex-variable framework.

Building on the previous work of Kou, Qian, and Pesenson, this study offers an effective method for determining the exact “bandwidth” (spectral radius) of a signal based solely on the properties of the operator.

Overall, this paper makes a sophisticated move by bringing hypercomplex analysis closer to modern probability and harmonic analysis.

Read the full paper here: https://link.springer.com/article/10.1007/s00041-025-10183-6